El año pasado, dicté algunos talleres de estadística y como siempre me gusta intercambiar ideas con los participantes, siempre aprendo algo nuevo de esas discusiones.
Uno de los participantes me comentaba que utilizaba para la construcción de las cartas de control de datos individuales el software Excel, a lo cual le dije que el Excel es una de las alternativas en el caso de no disponer algún software como por ejemplo Minitab.
Cuando hablamos sobre la forma de calcular los límites de control de las cartas individuales me dijo que lo hacía de la siguiente manera:
Límite inferior de carta de control: LCI = Xmedia – 3 DS
Límite superior de carta de control: LCS = Xmedia + 3 DS
Donde Xmedia es la media estimada del conjunto de datos y DS es la desviación estándar de ese mismo conjunto de datos.
Lo anterior es un enfoque correcto para calcular los límites del gráfico de control. La media estimada es simplemente la media del conjunto de datos, formada sumando los puntos de datos en el conjunto de datos y dividiendo por la cantidad de puntos de datos en el conjunto de datos. La desviación estándar estimada se calculó utilizando la desviación estándar de la muestra. En Microsoft Excel esto se obtiene usando la función STDEV y se calcula fácilmente. Aunque este no es el enfoque correcto.
El problema con el uso de la función STDEV de la muestra es que no tiene en cuenta la secuencia temporal de los datos. No importa cómo mezcle un conjunto de datos, seguirá teniendo la misma desviación estándar de la muestra. Entonces, lo que se requiere es una estimación de la desviación estándar que tenga en cuenta la secuencia de tiempo de los datos. En la práctica, esto se hace utilizando el rango móvil de los datos. Para dos puntos de datos consecutivos, el rango móvil es la diferencia absoluta entre los dos puntos de datos. Entonces, si el conjunto de datos tenía N puntos de datos, tendrá N-1 valores de rango móvil. La desviación estándar del conjunto de datos se puede estimar como:
DS = MediaRM / 1,128
Donde MediaRM es el promedio de los N-1 rangos móviles.
Cuando los datos se volvieron a representar en gráficos de control con los límites de control adecuados, las señales de fuera de control fueron claras.
Como nota al margen, el otro problema con el enfoque del graduado de MBA es que nunca construyó el gráfico de rango móvil, que es una serie de tiempo de los valores del rango móvil con un límite de control apropiado. En general, se acepta que es valioso mirar este gráfico, porque representa los mismos datos de una manera diferente y brindará otra vista de lo que está sucediendo en el proceso. Es fácil de construir con un software como Minitab junto con la tabla de valores individuales
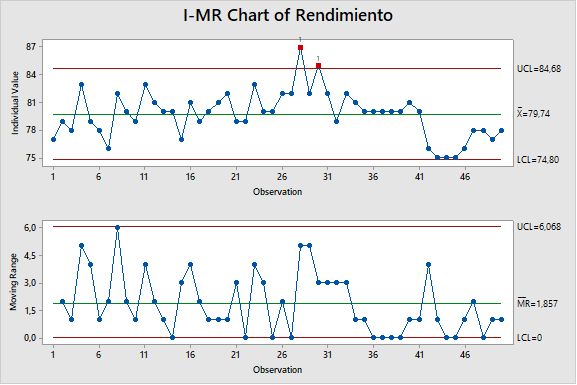
Les dejo un ejemplo (figura 1) donde ingresamos 50 datos individuales en Minitab y luego graficamos la carta de control I-RM (datos individuales – rango móvil).
De forma paralela ingresamos esos mismo datos en una planilla Excel y calculamos el valor promedio y la desviación estándar.
Podemos observar que los límites de control de la carta con Excel son más amplios debido a que el valor de desviación estándar calculado por Excel es mayor al calculado por Minitab de acuerdo a lo indicado anteriormente, por lo tanto los valores individuales que en la carta de control con minitab dieron fuera de control, en la carta construida con Excel están dentro de los limites.
La carta de valores individuales tiene límites de control más sensibles al cambio.
Otro tema a tener en cuenta es la construcción del gráfico de rango móvil, sumamente importante para ver las variaciones individuales a lo largo del proceso.
Figura 1
Cálculo x Excel
Promedio: 79,74
Desviación estándar: 2,5055856
LCS: 87,26
LCI: 72,22
Deje una Respuesta